2011年にNHKクロースアップ現代で取り上げられたこともあったらしいのですが
実はそれは見ていませんでした。
世界的なIT会社が新入社員の必読本に指定しているとか
この本にまつわる逸話にはいとまがないのですが
それを抜きにして非常に参考になる本です。
著者のG.ポリアは数学者ですが、数学的な問題に限らずに
あらゆる種類の問題を解決するためのヒントを提示してくれていることで素晴らしい本なのです。
わかりやすく説明するために数学の問題を例題にしてくれていると考えた方が良いかも知れません。
問題解決の4ステップが、以下の4つです。
第1のステップ 問題を理解すること
第2のステップ 計画を立てること
第3のステップ 計画を実行すること
第4のステップ ふり返ってみること
実は、私の娘は最近流行りの「数学ガール」で
この本にある例題に2人で盛り上がったこともありました。
例えば、61ページにあるこの問題です。
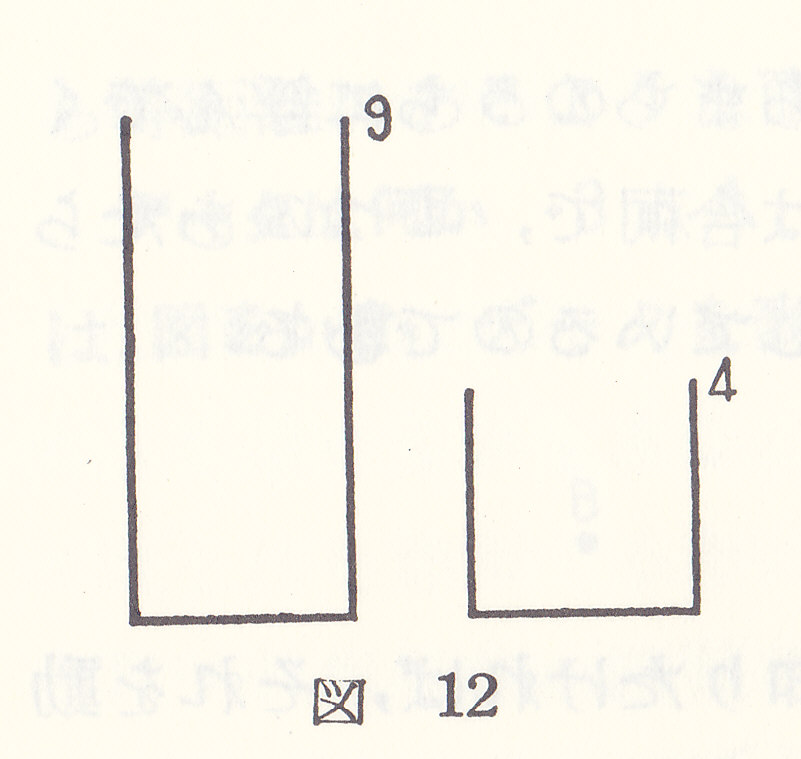
「われわれが4リットルと9リットルの2つの桶しかもっていないとき
ちょうど6リットルの川の水をくむのにはどうすればよいか。」
面白いのは、この例題が「逆向きにといていく」ことの説明に使われていることです。
ビジネスに応用される理由がここにあるのかも知れません。
「要求されているものから出発し、求めるものはすでに得られたと仮定せよ。」
「望みの結果はどんな前提から、導かれるかをたずねよう。」
今、私が日常に取り組んでいることと全く一緒です。
目的やビジョンを明らかにしたなら、そこにたどりつくためにあらゆる目標や手段を考え実行していく。
問題に対する、ヒントをお教えしましょう。
「われわれは大きな入れ物いっぱいに9リットルまで入れることができる。
6リットルを得るには、3リットルをすてればよい。
それは…小さい入れ物に1リットルあればよい!それがみそである。」
川の水は無限にあると考えてもらって
捨てて残すという作業を繰り返すことで
「1リットル」が得られるまで、いろいろやってみると良いのかも知れません。
未解答のままだと気持ちが悪いでしょうから、正解をお教えしますね。
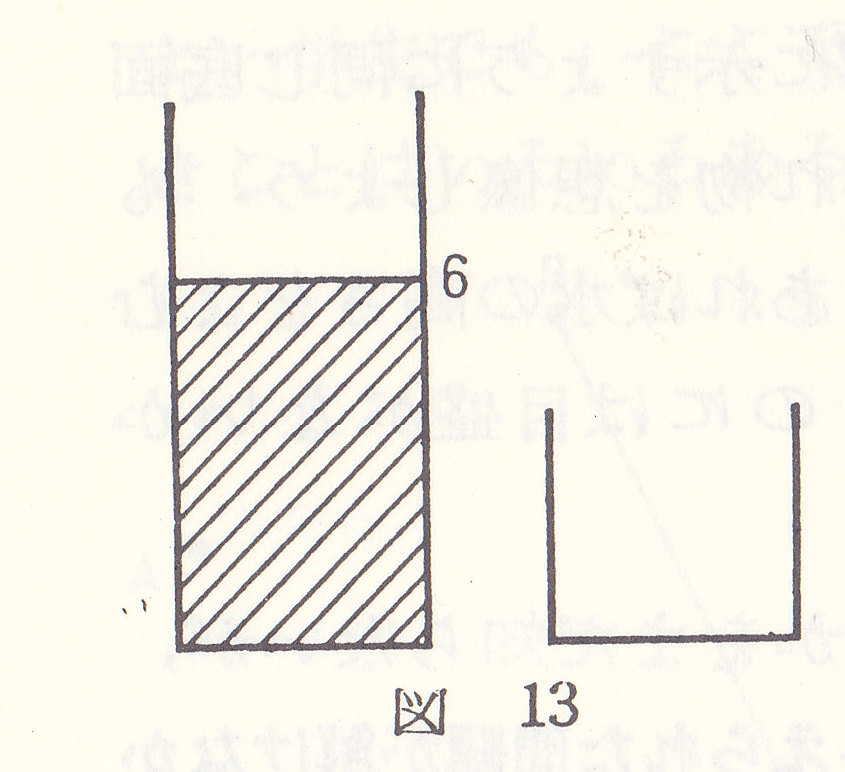
まず、大きな入れ物いっぱいに水を(9リットル)入れます。
この水を、4リットルの入れ物にうつして、川へ捨てます。
すると5リットルの水が残りますね。
大きな入れ物に残った水5リットルに対して、これをもう1回繰り返すと
1リットルの水が大きい入れ物に残ることになります。
9リットル - 4リットル = 5リットル
5リットル - 4リットル = 1リットル
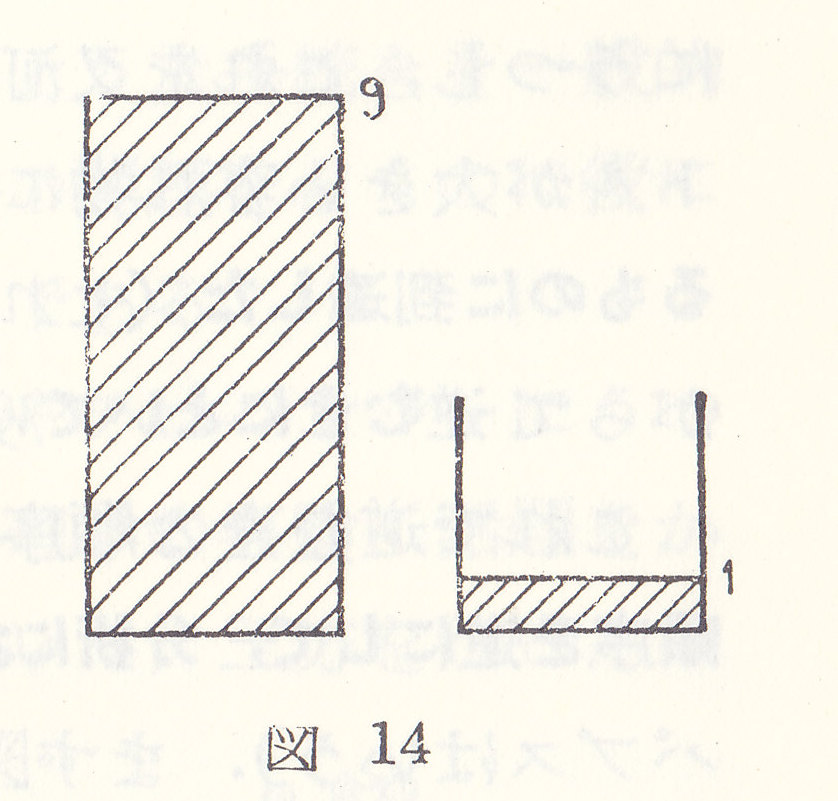
その1リットルの水を小さい入れ物にうつします。
そのうえで大きい入れ物に9リットルを準備して、1リットルが入った小さな入れ物にうつします。
9リットル - (4リットル - 1リットル) = 6リットル
そこで大きな入れ物に残った水は6リットルになります。
面白いですよね!
映画ダイハード地下鉄編にも似たようなクイズがあったのを思い出しました。
実は、この本で最も興味をもったのは「発見学」という概念で章をたてていることです。
次の言葉に感銘を受けました。
「野心的な問題はそれが単にみせかけではなく
直接目にみえるものの背後にひそむ何かの見通しに根ざすかぎり
成功の機会にめぐまれているのである。」
わかりにくい言葉なので、その前出の言葉に言い換えれば
「野心的な計画の方が成功の機会にめぐまれている。」
勇気が沸いてくる言葉です。